|
|
 |
Dat Ngo, Gorden Videen, Petr Chylek: A FORTRAN code for the scattering of EM waves by a sphere with a nonconcentric spherical inclusion. Computer Physics Comunications 99(1996) 1, 94-112.
Available from the CPC International Program Library.
Program in TurboPascal, TurboC or FORTRAN 95 by E. B. Shybanov, and V. I. Haltrin to compute scattering by large spherical particles.
Program to calculate the scattering from a sphere containing a nonconcentric spherical inclusion.
This program was written by Dat Ngo. It follows the derivation of Ngo, Videen and Chylek given in Computer Physics Communications 1077, p. 94-112 (1996).
Monte Carlo software and MATLAB toolbox for simulating light transport in biological tissue-

Mathcad programme of the Mie theory by Michael Knappmann.
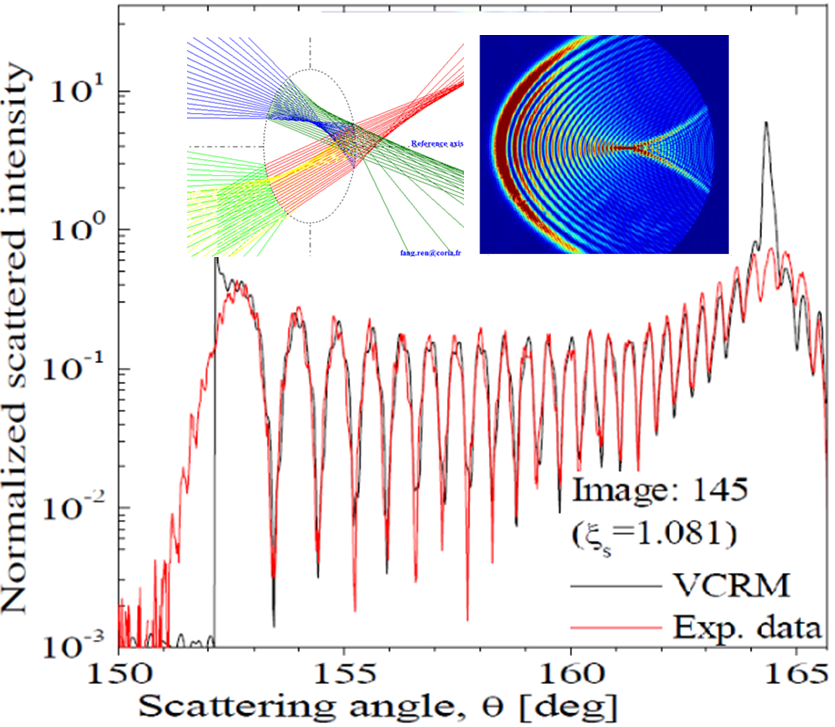
VCRMEll2D
VCRMEll2D by Kuan Fang Renis the first realization of the Vectorial Complex Ray Model - VCRM developed by the author. By introducing the property of the Wavefront in the geometrical optics model, the VCRM can calculate very precisely the interaction of a wave of any form with a object of smooth surface and size much larger than the wavelength of the incident beam.
Semi-emperical model of absoption and scattering by isotropic fractal aggragates of spheres.
MySimLabs is a web site presenting some Open Source MATLAB tools for simulating how light interacts with opaque surfaces, using Monte Carlo ray-tracing methods by David Bergström.
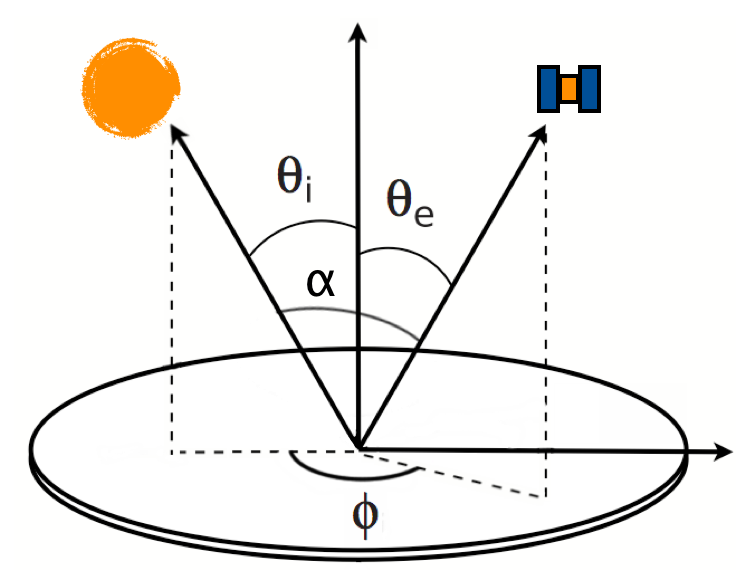
Program for the Analysis of a Laser Beam Focused Within an Aerosol Spray (FLSPRY) for theoretical analysis of the propagation of a laser pulse optically focussed within an aerosol spray.
Siris is a ray-optics light-scattering Fortran program by Karri Muinonen.
|
|
 |
|